Estudo Funções Quadráticas
Estudo Funções Quadráticas
Função quadrática é toda a função que pode ser definida por um polinómio de 2º grau numa variável.

Estudo da concavidade de uma função quadrática
Se a >0, concavidade é voltada para cima
Se a<0, concavidade é voltada para baixo.

Intersecção com os eixos coordenados
Zeros de uma função quadrática

Os zeros de uma função quadrática representam os valores de x para os quais a função tem imagem igual a zero. f(x) =0.

Função quadrática, forma canónica
Fórmula resolvente, permite calcular os zeros das funções quadráticas
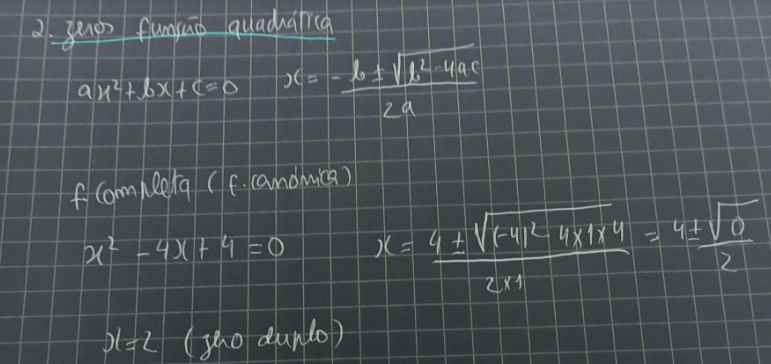
Exemplo de aplicação da fórmula resolvente:
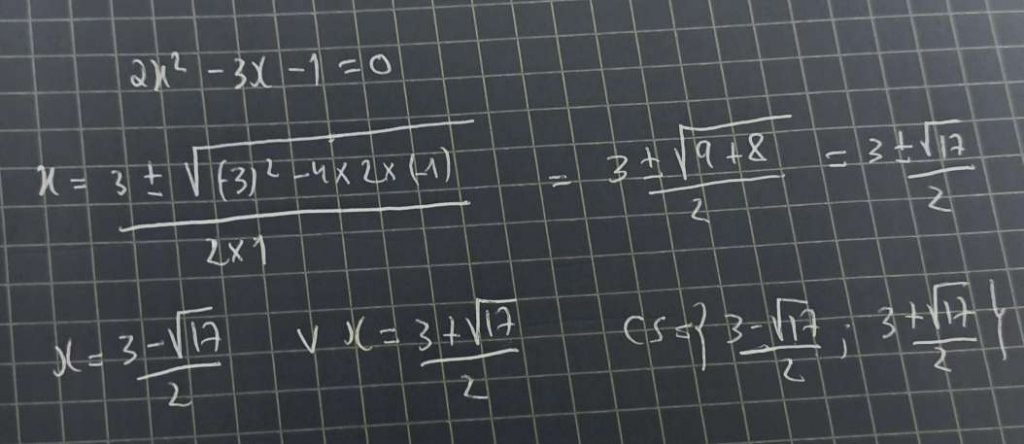
Binómio Discriminante, conhecido com delta
Ele é o que está dentro da raiz quadrada da fórmula resolvente
Binómio Discriminante indica-nos o nº de zeros e o estudo do sinal
O seu valor faz depender o nº de zeros existente daí o considerarmos discriminante.
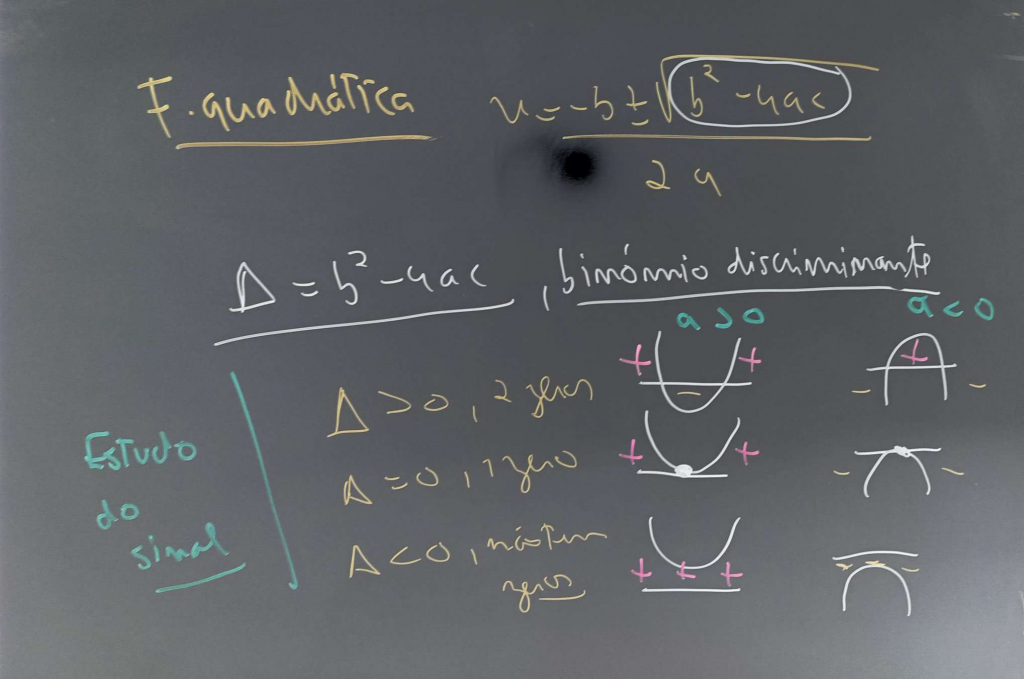
Cálculo de zeros em funções quadráticas incompletas
Existem casos de funções quadráticas que sendo incompletas se podem resolver por outras formas diferentes:
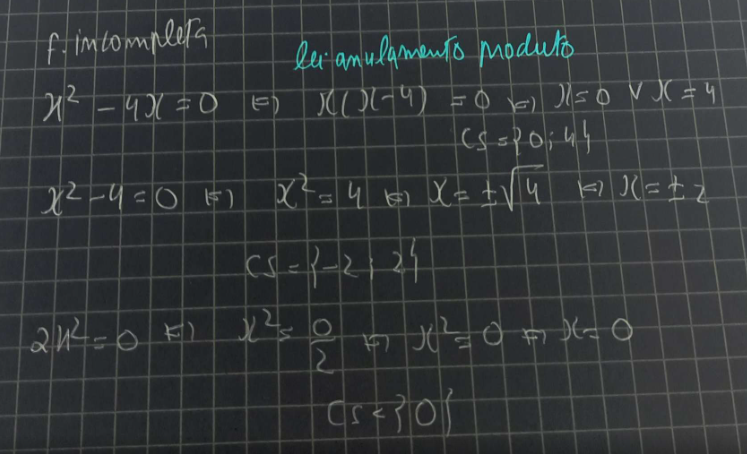
Exercícios de revisão
Método 2
Exemplos de aplicação
Exemplo 1.
Exemplo 2.
Exemplo 3
Exemplo 4

Atenção às diferenças
Exercícios de revisão
Vértice de uma função quadrática

Relação entre vértice e contradomínio de uma função

Vértice de uma função quadrática

Translação de uma função quadrática pelo respectivo vértice

Estudo da monotonia e vértice de uma função

Veja também – Zeros de uma função quadrática

Ver também
site da nossa empresa: http://kids.com.pt
Pretende aulas de apoio – Contacte-nos: 91 818 70 95