Estudo da função afim
Estudo da função afim
Estudo do domínio e contradomínio
A função Afim representa uma reta tem dessa forma domínio e contradomínio IR.
A função Afim é do tipo y = ax + b
o a representa o declive da função e o b é a ordenada na origem ou f(0), ponto de intersecção com o eixo Oy.
Declive da função afim.
O valor de a representa o declive da função consoante o valor de a, assim temos:
a<0, f é estritamente decrescente
a>0, f é estritamente crescente
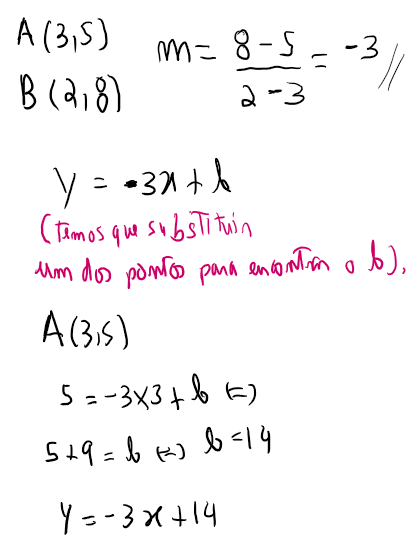
Ordenada na origem é o ponto da função que intersecta o eixo Oy, representa f(0) ou a imagem do zero.
ESTUDO DO DECLIVE DE UMA FUNÇÃO AFIM DADOS 2 PONTOS
A (x1,y1) e B(x2,y2)
a = (y2 -y1)/(x2-x1)
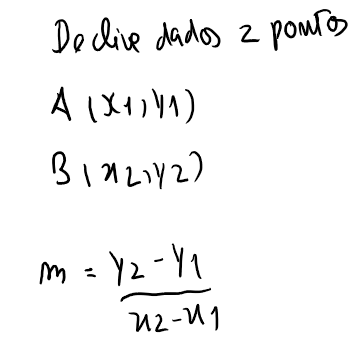
Estudo da ordenada na origem dados 2 pontos
Quando o valor de b ou da ordenada na origem é igual a zero significa que esta passa no ponto de origem (0,0).
Assim é do tipo y =ax (é uma função linear)
Relação entre o declive e a monotonia da função afim
De acordo com o declive da função temos:
Quando a >0 f é estritamente crescente em IR.
Quando a <0, f é estritamente decrescente em IR.
Em resumo: quando a função tem declive positivo é monótona crescente e quando tem declive negativo é monótona decrescente.
Zeros da função Afim
Os zeros de uma função representam os valores de x para os quais a imagem é zero. f(x) = 0 ou y.
Representa a intersecção da função com o eixo Ox.
Desta forma temos y = 0 <=> ax + b = 0 <=> x = -b/a
Por exemplo: y = 3x + 1 <=> 3x +1 =0 <=> 3x = -1 <=> x = -1/3
Estudo do sinal de uma função Afim
Exemplo de estudo de uma função Afim
Duas retas dizem-se paralelas quando têm o mesmo declive
Estudo de uma função afim: zeros, sinal, monotonia, Df e D’f.
Exemplo de aplicação
Exercícios de revisão
Exercício nº 1
Exercício nº 2
Exercício nº 3
Exercício nº 4
Se pretender apoio escolar online contacte-nos:
Caderno de Apoio Matemática 10º ano
Veja mais – Matemática 10º ano
https://pt.wikipedia.org/wiki/Fun%C3%A7%C3%A3o_afim